L2-CAF: A Neural Network Debugger
Every software engineer has used a debugger to debug his code. Yet, a neural network debugger… That’s news! This paper [1] proposes a debugger to debug and visualize attention in convolutional neural networks (CNNs).
Before describing the CNN debugger, I want to highlight few attributes of program debuggers (e.g., gdb): (I) Debuggers are not program-specific, i.e., we use the same debugger to debug many programs; (II) We use a debugger to debug a few lines in our code, i.e., not every line; (III) Before using a debugger, we decide consciously which part of the program we want to debug (e.g., which function); this is where we set our breakpoints; (IV) A debugger helps us understand a program by pausing its execution at a breakpoint (e.g., S1), then executing a few instructions till another point (e.g., S2). By inspecting the key changes between S1 and S2, we understand our code. Figure 1 illustrates how a debugger helps us execute a few instructions between two points in our program: S1 & S2.
We tend to regard neural networks as black boxes. Can’t we design a debugger neural network to interpret these black boxes?! I believe this is possible. L2-CAF [1] is a tiny neural network — of size 7x7 — that can visualize attention in neural networks. L2-CAF (I) supports a large spectrum of architectures; (II) visualizes attention at both the last and intermediate convolutional layers, i.e., can debug various parts inside a given network; (III) Before using L2-CAF, we decide consciously which part of the network we want to debug (e.g., which layer); (IV) L2-CAF helps us understand a network by monitoring its execution between two points (S1 and S2), then identifying the key features between these two points. Figure 2 illustrates how L2-CAF debugs a CNN.
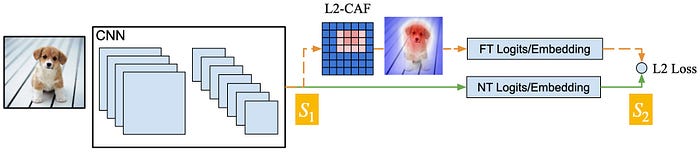
Given a trained CNN as shown in Figure 2, L2-CAF feeds an input image x through a normal feed-forward pass (green solid path) to generate the network output NT(x). Then, L2-CAF feeds x again but multiplies the last convolutional feature map by a filter f (orange dashed path) to generate a new filtered output FT(x,f). L2-CAF optimizes f using gradient descent to minimize the difference between NT(x) and FT(x, f) while constraining the L2-Norm of the filter f.
Formally speaking, L2-CAF casts attention visualization as a constrained optimization problem. It leverages the L2-Norm Constraints as an Attention Filter, and hence the name L2-CAF. L2-CAF solves the following constraint optimization problem using gradient descent. For those comfortable with optimization problems, the following equation should be familiar
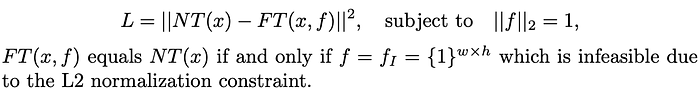
Figure 4 depicts the Hadamard (element-wise) multiplication between the convolutional feature maps and the L2-CAF. In standard architectures, the last convolutional feature maps A has K channels and 7x7 spatial dimensions. Accordingly, L2-CAF is a filter with a size of 7x7. If L2-CAF is all ones, the objective function ||NT(x)-FT(x,f)|| equals zero, but the L2-Norm constraint is violated — ||f||_2 = sqrt(49) = 7. In contrast, If L2-CAF identifies the key features in A, the L2-Norm constraint is satisfied (||f||_2=1) and ||NT(x)-FT(x,f)|| is minimum.
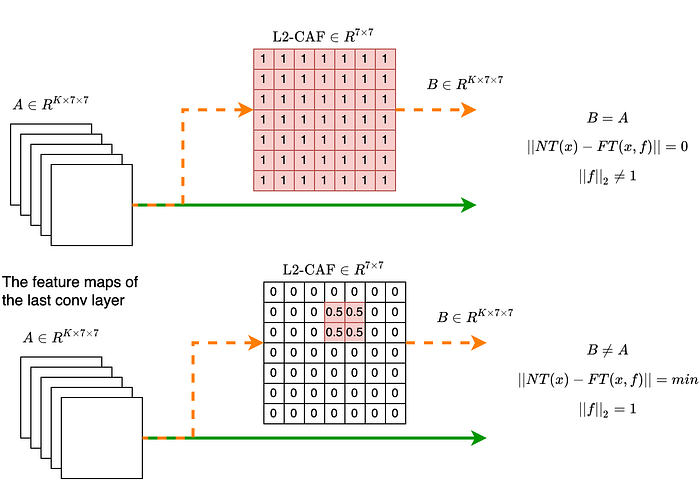
To debug a CNN, L2-CAF leverages gradient descent to identify the key features inside the feature maps. Gradient descent guides L2-CAF to find the optimal filter f that minimizes the loss function ||NT(x)-FT(x,f)|| while satisfying the L2-Norm constraint. The L2-Norm constraint has two benefits. The first benefit is that it avoids a trivial solution where L2-CAF converges to all ones and concludes that all features are equally important as shown in Figure 4 (Top).
The second benefit of the L2-Norm constraint is that it supports multiple modes. Accordingly, L2-CAF can attend to multiple locations at the same time. That is important when an image contains multiple objects at different locations as shown in Figure 5.

The L2-CAF network comes in two different flavors: class-oblivious and class-specific. The class-oblivious L2-CAF is best for feature embedding networks (e.g., retrieval and representation learning networks). These networks output a feature embedding with d dimensionality where each dimension represents an aspect of the network input. In contrast, the class-specific L2-CAF is best for classification networks. The class-specific L2-CAF can generate a heatmap for each output logit (different classes) making it perfect for images with multiple distinct objects as shown in Figure 6.

When debugging our code, we can set our breakpoints at any point. Similarly, L2-CAF can set its breakpoints at different parts of the network. Accordingly, L2-CAF visualizes attention in both the last and intermediate convolutional layers. Figure 7 shows how L2-CAF can visualize two objects simultaneously in a given image. L2-CAF delivers coarse-grained attention when applied on the last conv layer, and fine-grained attention when applied on an intermediate conv layer.

Finally, I hope this article has delivered the following key point: We can understand a neural network by debugging it, like the way we debug our source code. L2-CAF is the first neural network debugger, but further extensions are required.

References
[1] Taha, A., Yang, X., Shrivastava, A. and Davis, L. A Generic Visualization Approach for Convolutional Neural Networks. ECCV 2020.
