Cross-Iteration Batch Normalization

This paper [1] leverages two simple ideas to solve an important problem. The paper solves the problem of batch normalization when the batch size b is small, e.g., b=2. Small batch size is typical for an object-detection network where the input image size is 600–1024 pixels and the network has expensive operations such as the feature pyramid network (FPN).

The paper [1] proposes batch-normalization across mini-batch iterations. This is difficult because the normalization statistics (mean and std) change across iterations. We cannot accumulate the statistics naively across iterations because the network weights change between iterations. Formally, the paper solves the following problem: given the batch-norm statistics at a previous iteration for a given input, can we estimate the corresponding batch-norm statistics at the current iteration? This problem is summarized in the following figure

Given batch-norm statistics (mean and std) at a previous iteration t-1, what is the corresponding batch-norm statistics at the current iteration t? The batch-norm statistics change for the same image-batch because the network weights change between iterations.

To solve this problem efficiently, the paper leverages two simple ideas. I will explain these two ideas using toy examples. Then, I will apply these two ideas for cross-iteration batch normalization (CBN).

Simple Idea #1: Taylor polynomial

Taylor polynomial has many applications; one application is to compute a function at one point given the function’s value at a nearby point. For instance, let f(x)=x² be our toy function. Taylor polynomial helps us estimate f(2.1) given our knowledge that f(2)=4. To achieve this, let's write the Taylor polynomial of our function

Using Taylor polynomial, we compute f(2.1) given our knowledge of f(x), f’(x), and f(2)=4.

Before moving to the next idea, it is worth noting that the Taylor polynomial estimation worked because 2.1 is close to 2. We cannot estimate f(0) using f(2) because the last term in Eq.2 would be too big to ignore. The next figure presents a visual illustration of this point.

The Taylor polynomial approximates a function f(x+δ) given the function’s value at nearby point x. Accordingly, the Taylor polynomial estimates are accurate in the green circle, e.g., f(2.1) and δ=0.1. If we use the Taylor polynomial to estimate f(0), we would get f(0)=-4 which is wrong. This happens because the difference between {0,2} is big, i.e., δ=2.

Simple Idea #2: Efficient Gradient Calculation

To apply the Taylor polynomial for cross-iteration batch normalization (CBN), we need to compute the gradient, i.e., f`(x). Computing the gradient is an expensive operation. However, the paper shows that this operation is cheap for certain operations, e.g., convolutional. Again, we will illustrate this point using a toy example before applying it on CBN. Let x=θ y be a simple matrix operation where θ is a column vector ∈ R² and y is a row vector ∈ R², and accordingly, x is a 2x2 matrix; the gradient of x with respect to θ has 2x2x2 elements. Yet, A detailed inspection shows that most of these elements are always zero. Accordingly, the cost of the gradient operation is lower than expected as shown in the next figure

A matrix multiplication operation using a toy example x=θ y. While the gradient has 2x2x2=8 elements, half of these elements are always zero — no need to compute them! The computational cost of the gradient is less than expected.

Now, it is time to apply both Taylor polynomial and efficient gradient ideas for cross-iteration batch normalization (CBN). Using Taylor polynomial, CBN uses the batch norm statistics from previous iterations to estimate the equivalent batch-norm statistics at the current iteration as follows

Using the Taylor polynomial, CBN computes the batch-norm statistics at the current iteration using the batch-norm statistics at a previous iteration.

This Taylor polynomial approximation works because — as mentioned in the paper — “We observe that the network weights change smoothly between consecutive iterations, due to the nature of gradient-based training.” This means that the difference between θ_t and θ_{t-τ} is negligible.

The smooth weights-change is an important assumption for cross-iteration batch normalization, but it is not the only assumption. The paper makes another assumption to compute the Taylor polynomial’s gradient. The gradient of the batch statistics depends on the weights θ in all preceding layers which is computationally expensive. However, It is found empirically that the gradient from earlier layers rapidly diminishes. Thus, the paper truncates these partial gradients at layer l as shown in the next figure

The gradient of batch-norm statistics depends on all preceding layers; it is computationally expensive. According to CBN, the partial gradients — from earlier layers — rapidly diminish. Motivated by this phenomenon, the paper truncates these partial gradients at layer l.

With an approximate gradient, the Taylor polynomial becomes

Instead of an exact gradient, an approximate gradient is used in the Taylor polynomial to reduce the computational complexity.

Please recall that this Taylor polynomial works only when the difference between weights (θ_t - θ_{t-τ}) is small. This requirement enforces two constraints: (I) CBN aggregates the batch statistics across a small number of iterations because the difference between weights θ_t and θ_{t−τ} increases as the number of iterations increases; Empirically, CBN is found effective with a window size up to k = 8 iterations, (II) The window size k should be kept small at the beginning of training, when the network weights change rapidly. Accordingly, CBN introduces a burn-in period where the window size k=1. The burn-in period is set to 25 epochs on ImageNet image classification and 3 epochs on COCO object detection.

Now, the Taylor polynomial approximation is reduced to the bare minimum; it is time to quantify its cost. The gradient term dμ/dθ is the most expensive term. Using the efficient gradient computation idea, the paper highlights the difference between the expected and the actual cost of the Taylor polynomial gradient. For a convolutional layer, the gradient’s expected-cost is O(C_out x C_out x C_in x K) where C_out and C_in denote the output and input channel dimension of the l-th layer, respectively, and K denotes the kernel size. Yet, the paper shows that the gradient’s actual-cost is O(C_out x C_in x K). The actual-cost is significantly smaller because the gradient is mostly zero as shown in the next equation

The batch-norm mean gradient with respect to the network’s weight is mostly zero. This is illustrated in Appendix B.

Using both Taylor polynomial and efficient gradient computation, CBN outperforms other batch-normalization techniques (e.g., Group batch norm) on small mini-batches. The next figure compares CBN with different batch normalization techniques using different minibatch sizes.

Top-1 classification accuracy vs. batch sizes per iteration. The base model is a ResNet-18 trained on ImageNet. The accuracy of vanilla batch normalization (BN) drops rapidly with small batch sizes. Batch Renormalization (BRN) stabilizes BN a little but still suffers from small batch sizes. Group-Batch Norm (GN) exhibits stable performance but underperforms BN on adequate batch sizes. Cross-iteration batch norm (CBN) compensates for the reduced batch size per GPU by exploiting approximated statistics from recent iterations (Temporal window size denotes how many recent iterations are utilized for statistics computation). CBN shows relatively stable performance over different batch sizes. Naive CBN, which directly calculates statistics from recent iterations without compensation, is shown not to work well.

The next table presents the classification performance on ImageNet using multiple batch sizes. CBN achieves comparable performance to other normalization baselines when using a large batch size (e.g., b=32). Yet, CBN is consistently better when using a small batch size (e.g., b=2).

Top-1 accuracy of normalization methods with different batch sizes using ResNet-18 as the base model on ImageNet.

CBN is particularly handy for object detection and semantic segmentation where a small batch size (e.g., b=4) is the default. The next table evaluates CBN using object detection task and COCO dataset.

Results of feature normalization methods on Faster R-CNN with FPN and ResNet50 on COCO.

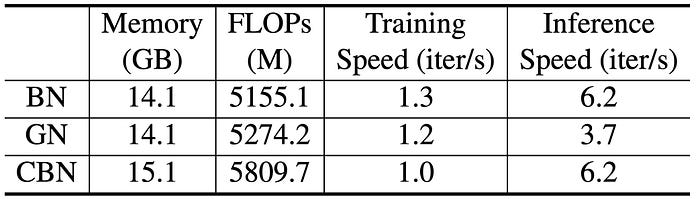
In terms of training/inference speed, the next table shows that the training speeds of CBN, BN, and GN are comparable. Yet, the inference speed of CBN is equal to BN, which is much faster than GN.

Comparison of theoretical memory, FLOPs, and practical training and inference speed between original BN, GN, and CBN in both training and inference on COCO.

My Comments

• The paper is well-written and the code is released. It is good to see that MSR-Asia allowed code release!
• The authors delivered a ton of experiment and ablation studies in the paper. I highly recommend reading the paper to learn more about CBN.
• In the ablation studies section, The author made an interesting conjecture. It is argued that vanilla BN might be suffering on small batch-size in later stages of training only! If I understand this correctly, vanilla BN is useful at the early stage of training even with a small batch size!! then, BN breaks at the later stage of training. I wish the author elaborated more on this.

References

[1] Yao, Zhuliang, Yue Cao, Shuxin Zheng, Gao Huang, and Stephen Lin. “Cross-iteration batch normalization.” CVPR 2021.